Metric Based Few-Shot Graph Classification
Abstract
Many modern deep-learning techniques do not work without enormous datasets. At the same time, several fields demand methods working in scarcity of data. This problem is even more complex when the samples have varying structures, as in the case of graphs. Graph representation learning techniques have recently proven successful in a variety of domains. Nevertheless, the employed architectures perform miserably when faced with data scarcity. On the other hand, few-shot learning allows employing modern deep learning models in scarce data regimes without waiving their effectiveness. In this work, we tackle the problem of few-shot graph classification, showing that equipping a simple distance metric learning baseline with a state-of-the-art graph embedder allows to obtain competitive results on the task. While the simplicity of the architecture is enough to outperform more complex ones, it also allows straightforward additions. To this end, we show that additional improvements may be obtained by encouraging a task-conditioned embedding space. Finally, we propose a MixUp-based online data augmentation technique acting in the latent space and show its effectiveness on the task.
Introduction
Graphs have ruled digital representations since the dawn of Computer Science. Their structure is simple and general, and their structural properties are well studied. Given the success of deep learning in different domains that enjoy a regular structure, such as those found in computer vision (Baumgartner et al. 2017; J. Zhang et al. 2019; Smirnov and Solomon 2021) and natural language processing (Brown et al. 2020; Mikolov et al. 2013; Vaswani et al. 2017; Devlin et al. 2019), a recent line of research has sought to extend it to manifolds and graph-structured data (Bronstein et al. 2017; Hamilton, Ying, and Leskovec 2017; Battaglia et al. 2018). Nevertheless, deep learning expressivity comes at a cost: deep models require vast amounts of data to search the complex hypothesis spaces they define. When data is scarce, these models end up overfitting the training set, hindering their generalization capability on unseen samples. While annotations are usually abundant in computer vision and natural language processing, they are harder to obtain for graph-structured data due to the impossibility or expensiveness of the annotation process (Hu et al. 2020; Sun et al. 2020). This is particularly true when the samples come from specialized domains such as biology, chemistry and medicine (Hassani 2022), where graph-structured data are ubiquitous. For instance, drug testing requires expensive in-vivo and laborious wet experiments to label drugs and protein graphs (Ma et al. 2020).
To address this problem, the field of Few-Shot (FS) learning (Fei-Fei, Fergus, and Perona 2006; Fink 2004) aims at designing models which can effectively operate in scarce data scenarios. While there has been some interest in FS node classification and link prediction, graph-level classification has mostly been overlooked in the FS setting. A general, high-level strategy for learning with little data consists of extracting knowledge from a related domain where the available data is enough to learn a reliable hypothesis and then adapt it to the task of interest. The latter is usually called the target task, while the data abundant one is denoted as source. When the task of interest is classification, categories from the source task are said to be base classes, while those of the target are called . Distance metric learning techniques have proven to be particularly effective for the problem, as samples embedded in a lower-dimensional space need fewer data to be discriminated. Among these methods, Prototypical Networks (Snell, Swersky, and Zemel 2017) has been one of the most successful, obtaining remarkable results in various tasks without waiving its simplicity. Surprisingly, versions of it have been derubricated to baseline in other existing FS graph classification works without much relevance. We confute in this work these misconceptions, showing that we can obtain competitive results in the task by equipping Prototypical Networks with a state-of-the-art graph embedder.
As typical in FS learning, we frame tasks as episodes, where an episode is defined by a set of classes and several supervised samples (supports) for each of them (Vinyals et al. 2016a). Such an episode is depicted in . While a standard Prototypical Network would embed the samples in the same way independently of the episode, we take inspiration from (Oreshkin, López, and Lacoste 2018) and empower the graph embeddings by conditioning them on the particular set of classes seen in the episode. This way, the intermediate features and the final embeddings may be modulated according to what is best for the current episode.
Given the insufficiency of the data to allow learning meaningful features for the target task from scratch, a learning model will often represent samples from the novel classes as a rearrangement of features from the data-abundant base classes. To this end, we propose a novel online data augmentation technique that creates artificial samples from two existing ones as a mixup of their latent representations. Training on these mixups of samples from the base classes forces the model to expect combinations of the base samples already at training time.
In summary, our contribution is three-fold:
Showing that a distance metric learning approach, while simple, works better than more complex meta-learning approaches for the task of FS graph classification;
Equipping the architecture with an episode-adaptive module, enhancing its expressivity to obtain more dynamic representations;
Suggesting a novel online data augmentation technique that creates new artificial samples in the latent space, showing a significant performance gain.
All our results are general and apply equivalently to any kind of graph family considered. All our code is available for research purposes. [^1].

Related work
Graph Representation Learning
Given graphs expressive power, graph-based modeling is ubiquitous in a variety of domains, ranging from social networks (Fan et al. 2022; Monti et al. 2019) to chemistry (Duvenaud et al. 2015; Fout et al. 2017; Stokes et al. 2020). In the graph representation learning context, the focus is on finding the best possible representation for these data structures: it usually involves the learning of a mapping between the discrete graph space and a continuous latent one in \(\mathbb{R}^d\) that should encode both topological features and signal possibly defined over nodes or edges. These features are usually obtained by graph convolutions (Kipf and Welling 2017; Velickovic et al. 2018). Due to its theoretical expressive power, we employ a Graph Isomorphism Network (Xu et al. 2019) as graph embedder. While the essence of supervised DL approaches requires large volumes of annotated data to learn from (Lake et al. 2017), the intrinsic structural complexity of graphs and their application in very specialized fields often give rise to annotation problems. When this happens, the too few supervised samples are not enough to fit the deep models, consequently hindering their performances.
Few-Shot Learning
FS learning has gained attention as a means to tighten the gap between machine learning models and human-like learning capability. In fact, the capacity to generalize from few examples is an hallmark of human intelligence already from infancy, as children can, for example, learn words they have heard only once (Carey and Bartlett 1978). In practice, several high-level paradigms are used in literature to solve tasks in a FS scenario: transfer learning techniques (Liu et al. 2018; Luo et al. 2017) aim at transferring the knowledge gained from a data-abundant task to a task with scarce data; ii) meta-learning (Finn, Abbeel, and Levine 2017; Yoon et al. 2018; Ravi and Larochelle 2017) techniques more generally introduce a meta-learning procedure to gradually learn meta-knowledge that generalizes across several tasks; iii) data augmentation works (Wu et al. 2018; Gao et al. 2018; Tsai and Salakhutdinov 2017) seek to augment the data applying transformations on the available samples to generate new ones preserving specific properties. We refer the reader to (Yaqing Wang et al. 2020) for an extensive treatment of the matter. Particularly relevant to our work are distance metric learning approaches: in this direction, (Vinyals et al. 2016a) suggest embedding both supports and queries and then labeling the query with the label of its nearest neighbor in the embedding space. By obtaining a class distribution for the query using a softmax over the distances from the supports, they then learn the embedding space by minimizing the negative log-likelihood. (Snell, Swersky, and Zemel 2017) generalize this intuition by allowing \(k\) supports for class to be aggregated to form prototypes. Given its effectiveness and simplicity, we chose this approach as the starting point for our architecture.
Graph Data Augmentation
Data augmentation follows the idea that in the working domain, there exist transformations that can be applied to samples to generate new ones in a controlled way (e.g., preserving the sample class in a classification setting while changing its content). Therefore, synthetic samples can meet the needs of large neural networks that require training with high volumes of data (Yaqing Wang et al. 2020). In Euclidean domains (e.g., images), this can often be achieved by simple rotations and translations (Benaim and Wolf 2018; Santoro et al. 2016). Unfortunately, in the graph domain, it is challenging to define such transformations on a given graph sample while keeping control of its properties. To this end, (Park, Shim, and Yang 2022; Yiwei Wang et al. 2020; H. Guo and Mao 2021; Han et al. 2022) propose to augment graph data directly in the data space, while (Yiwei Wang et al. 2021) interpolates latent representations to create novel ones. We also operate in the latent space, but differently from (Yiwei Wang et al. 2021), we suggest creating a new sample by selecting only certain features of one representation and the remaining ones from the other by employing a random gating vector. This allows to obtain artificial samples that are randomly composed of the features of the existing samples, rather than a linear interpolation of their features.
Few-Shot Graph Representation Learning
FS graph representation learning is concerned in applying graph representation learning techniques in scarce data scenarios. Similarly to standard graph representation learning, it tackles tasks at different levels of granularity: node-level (Zhou et al. 2019; S. Zhang et al. 2019; Yao et al. 2019; N. Wang et al. 2020; Ding et al. 2020), edge-level (Baek, Lee, and Hwang 2020; Sheng et al. 2020; S. Wang et al. 2021; Lv et al. 2019) and graph-level (Z. Guo et al. 2021; Yaqing Wang et al. 2021; Chauhan, Nathani, and Kaul 2020; Ma et al. 2020; Jiang et al. 2021). In this work, we tackle the problem of FS graph classification. The first work to study graph classification in a FS setting can be traced to (Chauhan, Nathani, and Kaul 2020) (GSM). Its contributions resulted in a helpful baseline method and datasets for the following works in the literature. Following works adapted MAML (Finn, Abbeel, and Levine 2017) to the graph setting (Ma et al. 2020) and proposed a modified version of Prototypical Networks leveraging domain specific priors (Jiang et al. 2021). Differently from the latter, we do not make any such assumption and do not change the original loss function, obtaining superior performance.
Approach
Setting and Notation
In FS graph classification each sample is a tuple \((\mathcal{G}=(\mathcal{V},\mathcal{E}), y)\) where \(\mathcal{G}=(\mathcal{V},\mathcal{E})\) is a graph with node set \(\mathcal{V}\) and edge set \(\mathcal{E}\), while \(y\) is a graph-level class. Given a set of data-abundant base classes \(C_{\text{b}}\), we aim to classify a set of data-scarce novel classes \(C_{\text{n}}\). We cast this problem through an episodic framework (Vinyals et al. 2016b): during training, we mimic the FS setting dividing the base training data in episodes. Each episode e is a \(N\)-way \(K\)-shot classification task, with its own train (\(D_{\text{train}}\)) and test (\(D_{\text{test}}\)) data. For each of the \(N\) classes, \(D_{\text{train}}\) contains \(K\) corresponding support graphs, while \(D_{\text{test}}\) contains \(Q\) query graphs. A schematic visualization of an episode is depicted in .

Prototypical Network (PN) Architecture
We build our network upon the simple-yet-effective idea of Prototypical Networks (Snell, Swersky, and Zemel 2017), originally proposed for FS image classification. We employ a state-of-the-art Graph Neural Network (GNN) as node embedder, composed of a set of layers of GIN convolutions (Xu et al. 2019), each equipped with a MLP regularized with GraphNorm (Cai et al. 2021). In practice, each sample is first passed through a set of convolutions, obtaining a hidden representation \({h}^{(l)}\) for each layer. According to (Xu et al. 2019), the latter is obtained by updating at each layer its hidden representation as \[\begin{aligned} \label{GIN-agg} \mathbf{h}_v^{(l)} = {\rm MLP}^{(l)} \left( \left( 1 + \epsilon^{(l)} \right) \cdot \mathbf{h}_v^{(l-1)} + \sum\nolimits_{u \in \mathcal{N}(v)} \mathbf{h}_u^{(l-1)}\right).\end{aligned}\] where \(\epsilon^{(l)}\) is a learnable parameter. Following (Xu et al. 2018), the final node \(d\)-dimensional embedding \(\mathbf{h}_v \in R^{d}\) is then given by the concatenation of the outputs of all the layers \[\mathbf{h}_v = \text{CONCAT}\left( \left\{ \mathbf{h}_v^{(l)} \right\}_{l=1}^{L} \right)\] where \(L\) is the total number of layers in the network. The graph-level embedding is then obtained by employing a global pooling function, such as mean or sum. While the sum is a more expressive pooling function for GNNs (Xu et al. 2019), we observed the mean to behave better for the task in most considered datasets and will therefore be the aggregation function of choice when not specified differently. The \(K\) embedded supports \(\mathbf{s}_1^{(n)}, \dots, \mathbf{s}_K^{(n)}\) for each class \(n\) are then aggregated to form the class prototypes \(\mathbf{p}^{(n)}\), \[\mathbf{p}^{(n)} = \frac{1}{K} \sum_{k=1}^{K} \mathbf{s}_k^{(n)}\] In the same way, the \(Q\) query graphs for each class \(n\) are embedded to obtain \(\mathbf{q}_1^{(n)}, \dots, \mathbf{q}_Q^{(n)}\). To compare each query graph embedding \(\mathbf{q}\) with the class prototypes \(\mathbf{p}_1, \dots, \mathbf{p}_N\), we use an \(\mathcal{L}_2\)-metric scaled by a learnable temperature factor \(\alpha\) as suggested in (Oreshkin, López, and Lacoste 2018). We refer to this metric as \(d_{\alpha}\). The class probability distribution \(\boldsymbol{\rho}\) for the query is finally computed by taking the softmax over these distances \[\boldsymbol{\rho}_n = \frac{\exp \left( -d_{\alpha}(\mathbf{q}, \mathbf{p}_n) \right)}{\sum_{n'=1}^{N} \exp(-d_{\alpha}(\mathbf{q}, \mathbf{p}_{n'}))}. \label{eq:proto-class-distr}\] The model is then trained end-to-end by minimizing via SGD the log-probability \(\mathcal{L}(\phi) = -\log \boldsymbol{\rho}_n\) of the true class \(n\). We will refer to this approach without additions as PN in the experiments.
Task-Adaptive Embedding (TAE)
Until now, our module computes the embeddings regardless of the specific composition of the episode. Our intuition is that the context in which a graph appears should influence its representation. In practice, inspired by (Oreshkin, López, and Lacoste 2018), we condition the embeddings on the particular task (episode) for which they are computed. Such influence will be expressed by a translation \(\boldsymbol{\beta}\) and a scaling \(\boldsymbol{\gamma}\).
First of all, given an episode \(e\) we compute an episode representation \(\mathbf{p}_{\mathbf{e}}\) as the mean of the prototypes \(\mathbf{p}_n\) for the classes \(n = 1, \dots, N\) in the episode. We consider \(\mathbf{p}_{\mathbf{e}}\) as a prototype for the episode and a proxy for the task. Then, we feed it to a Task Embedding Network (TEN), composed of two distinct residual MLPs. These output a shift vector \(\boldsymbol{\beta}_\ell\) and a scale vector \(\boldsymbol{\gamma}_\ell\) respectively for each of the layers of the graph embedding module. At layer \(\ell\), the output \(\mathbf{h}_{\ell}\) is then conditioned on the episode by transforming it as \[h_{\ell}' = \boldsymbol{\gamma} \odot h_{\ell}+\boldsymbol{\beta}.\] As in (Oreshkin, López, and Lacoste 2018), at each layer \(\boldsymbol{\gamma}\) and \(\boldsymbol{\beta}\) are multiplied by two \(L_{2}\)-penalized scalars \(\gamma_{0}\) and \(\beta_{0}\) so to to promote significant conditioning only if useful. Wrapping up, defining \(g_{\Theta}\) and \(h_{\Phi}\) to be the predictors for the shift and scale vectors respectively, the actual vectors to be multiplied to the hidden representation are respectively \(\boldsymbol{\beta}= \beta_0 g_{\Theta}(\mathbf{e})\) and \(\boldsymbol{\gamma}= \gamma_0 h_{\Phi}(\mathbf{e}) + \mathbf{1}\). When we use this improvement in our experiments, we add the label TAE to the method name.
MixUp (MU) Embedding Augmentation
Typical learning pipelines rely on data augmentation to overcome limited variability in the dataset. While this is mainly performed to obtain invariance to specific transformations, we use it to improve our embedding representation, promoting generalization on unseen feature combinations. In practice, given an episode \(\mathbf{e}\), we randomly sample for each pair of classes \(n_1, n_2\) two graphs \(\mathcal{G}^{(1)}\) and \(\mathcal{G}^{(2)}\) from the corresponding support sets. Then, we compute their embeddings \(\mathbf{s}^{(1)}\) and \(\mathbf{s}^{(2)}\), as well as their class probability distributions \(\boldsymbol{\rho}^{(1)}\) and \(\boldsymbol{\rho}^{(2)}\) according to . Next, we randomly obtain a boolean mask \(\boldsymbol{\sigma} \in \{0,1\}^k\). We can then obtain a novel synthetic example by mixing the features of the two graphs in the latent space \[\tilde{\boldsymbol{s}} = \boldsymbol{\sigma} \mathbf{s}_{1} + (\mathbf{1} - \boldsymbol{\sigma}) \mathbf{s}_{2},\] where \(\mathbf{1}\) is a \(d\)-dimensional vector of ones. Finally, we craft a synthetic class probability \(\tilde{\rho}\) for this example by linear interpolation \[\tilde{\boldsymbol{\rho}} =\lambda \boldsymbol{\rho}^{(1)} + (1 - \lambda) \boldsymbol{\rho}^{(2)} \label{eq:linear-interpolation-distr}\] where \(\lambda = \left( \frac{1}{d} \sum\limits_{i=1}^{d} \boldsymbol{\sigma}_i \right)\) represents the percentage of features sampled from the first sample. If we then compute the class distribution \(\boldsymbol{\rho}\) for \(\mathbf{s}\) according to , we can ask it to be similar to by adding the following regularizing term to the training loss \[\mathcal{L}_{\text{MU}} = \| \boldsymbol{\rho} - \tilde{\boldsymbol{\rho}}\|_2^2.\] Intuitively, by adopting this online data augmentation procedure, the network is faced with new feature combinations during training, helping to explore unseen regions of the embedding space. The overall procedure is summarized in .

Experiments
Datasets
We benchmark our approach over two type of datasets: the first one was introduced in (Chauhan, Nathani, and Kaul 2020), and consists of:
TRIANGLES, a collection of graphs labeled \(i=1, \dots, 10\), where \(i\) is the number of triangles in the graph.ENZYMES, a dataset of protein tertiary structures from the BRENDA database (Chang et al. 2020); each label corresponds to a different top-level enzyme.Letter-High, a collection of graph-represented letter drawings from the English alphabet; each drawing is labeled with the corresponding letter.Reddit-12K, a social network dataset where graphs represent threads, with edges connecting users interacting. The label of a thread is given by the corresponding discussion forum.
We will refer to this set of datasets as \(\mathcal{D}_\text{A}\). The second set of datasets was introduced in (Ma et al. 2020), and consists of:
Graph-R52, a textual dataset in which each graph represents a different text, with words being connected by an edge if they appear together in a sliding window.COIL-DEL, a collection of graph-represented images obtained through corner detection and Delaunay triangulation.
We will refer to this set of datasets as \(\mathcal{D}_\text{B}\). The overall dataset statistics are reported in .
It is important to note that only the datasets in \(\mathcal{D}_\text{B}\) have enough classes to permit a disjoint set of classes for validation. In contrast, a disjoint subset of the training samples is used as a validation set in the first four by existing works. We argue that this setting is critically unfit for FS learning, as the validation set does not make up for a good proxy for the actual testing environment since the classes are not novel. Moreover, the lack of a reliable validation set prevents the usage of early stopping, as there is no way to decide on a good stopping criterion for samples from unseen classes. We nevertheless report the reports on this evaluation setting for the sake of comparison.
Baselines
We extensively compare our results to the other existing works in current literature, i.e. the pioneering work GSM (Chauhan, Nathani, and Kaul 2020), the current state-of-the-art method (AS-MAML) (Ma et al. 2020) and the most recent SMF-GIN (Jiang et al. 2021). As in (Ma et al. 2020), we decided to directly report the results included by the respective authors in their works.
GSM
As a first step, the authors compute graph prototypes and then cluster them based on their spectral properties to create super-classes. These are then used to generate a super-graph which is employed to separate the novel graphs. As previously stated, the class prototypes are computed from the spectral properties of the graphs rather than the average of their embeddings, as usually done in prototypical networks.
AS-MAML
This solution follows the meta-learning framework, and it is based on the popular Model-Agnostic Meta-Learning (MAML) architecture (Finn, Abbeel, and Levine 2017). The authors moreover propose a reinforcement learning-based adaptive step controller to improve the robustness of the graph meta-learner.
SMF-GIN
A GNN is employed to encode both global (attention over different GNN layer encodings) and local (attention over different substructure encodings) properties. We point out that they include a ProtoNet-based baseline. However, their implementation does not accurately follow the original one, and, differently from us, leverages domain specific prior knowledge.
Experimental details
Our graph embedder is composed of two layers of GIN followed by a mean pooling layer and the dimension of the resulting embeddings is set to \(64\). Furthermore, both the latent mixup regularizer and the L2 regularizer of the task-adaptive embedding are weighted at \(0.1\). The framework is trained with a batch size of \(32\) using Adam optimizer with a learning rate of \(0.0001\). We implement our framework with Pytorch Lightning (Falcon et al. 2019) using Pytorch Geometric (Fey and Lenssen 2019) and Wandb (Biewald 2020) to log the experiment results of the model. The specific configurations of all our approaches are reported in .
Results
Benchmark \(\mathcal{D}_\text{A}\)
As can be seen in , the proposed approach compares favorably in the large majority of the considered datasets. We obtain an overall margin of \(+7.24\%\) and \(+4.9\%\) accuracy compared to GSM (Chauhan, Nathani, and Kaul 2020) for \(k=5, 10\) respectively, while the improvements are \(+0.96\%\) and \(+0.86\%\) with respect to AS-MAML (Ma et al. 2020). We note that the latter are only computed over TRIANGLES and Letter-High, as the authors chose not to evaluate over the two remaining datasets in the \(\mathcal{D}_A\) benchmark. However, we again stress the partial inadequacy of these datasets as a realistic evaluation tool due to the lack of a disjoint set of classes for the validation set.
| TRIANGLES | Letter-High | ENZYMES | ||||||
| 5-shot | 10-shot | 5-shot | 10-shot | 5-shot | 10-shot | 5-shot | 10-shot | |
| GSM | 71.40 | 75.60 | 69.91 | 73.28 | 55.42 | \(\mathbf{60.64}\) | 41.59 | 45.67 |
| SMF-GIN | 79.85 | - | - | - | - | - | - | - |
| AS-MAML | \(86.47\) | 87.26 | 76.29 | 77.87 | - | - | - | - |
| PN+TAE+MU | \(\mathbf{87.47}\) | \(\mathbf{87.59}\) | \(\mathbf{77.21}\) | \(\mathbf{79.26}\) | \(\mathbf{56.86}\) | \(59.39\) | \(\mathbf{45.75}\) | \(\mathbf{48.55}\) |
Benchmark \(\mathcal{D}_\text{B}\)
Consistently, our approach yields significant improvements over both COIL-DEL and R-52. In fact, shows that the model obtains an average margin of \(+4.37\%\) and \(+4.53\%\) over AS-MAML (Ma et al. 2020) for \(k=5, 10\) respectively. Interestingly, a vanilla Prototypical Network (PN) architecture with the proposed graph embedder is already sufficient to obtain state-of-the-art results. The subsequent rows then show the efficacy of the proposed improvements. Task-adaptive embedding (TAE) allows obtaining the most critical gain, yielding an average increment of \(+2.82\%\) and \(+2.42\%\) for the \(5\)-shot and \(10\)-shot cases, respectively. Then, the proposed online data augmentation technique (MU) allows obtaining an additional boost, especially on COIL-DEL. In fact, in the latter case, its addition yields a \(+0.65\%\) and \(+1.72\%\) improvement in accuracy for \(k=5, 10\). We notice that on this benchmark we obtain a large margin of improvement w.r.t. the state of the art. These are also the datasets in which the evaluation has the more grounded setting, given the availability of a proper validation set.
| Graph-R52 | COIL-DEL | mean | ||||
| 5-shot | 10-shot | 5-shot | 10-shot | 5-shot | 10-shot | |
| AS-MAML | 75,33 | 78,33 | 81.55 | 84.75 | 78.44 | 81.54 |
| PN | \(73.11\) | \(78.04\) | \(85.57\) | \(87.28\) | \(79.34\) | \(82.66\) |
| PN+TAE | \(77.91\) | \(81.32\) | \(86.41\) | \(88.85\) | \(82.16\) | \(85.08\) |
| PN+TAE+MU | \(\mathbf{77.92}\) | \(\mathbf{81.57}\) | \(\mathbf{87.7}\) | \(\mathbf{90.57}\) | \(\mathbf{82.81}\) | \(\mathbf{86.07}\) |
Qualitative analysis
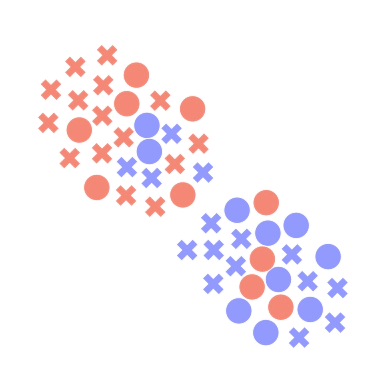
The latent space learned by the graph embedder is the core element of our approach since it determines the prototypes and the subsequent sample classification. To provide a better insight into our method peculiarities, depicts a T-SNE representation of the learned embeddings for novel classes. Each row represents different episodes, while the different columns show the different embeddings obtained with our approach and its further refinements. We also highlight the queries (crosses), the supports (circles) and the prototypes (star). As can be seen, our approach separates samples belonging to novel classes into clearly defined clusters. Already in PN model, some classes naturally cluster in different regions of the embedding. The TAE regularization improves the class separation without changing the disposition of the cluster in the space significantly. Our insight, is that the context may let the network reorganize the already seen space, without moving far from the already obtained representation. Finally, MU allows better use of previously unexplored regions, as expected from this kind of data augmentation. We show that our feature recombination helps the network better generalize and anticipate the coming of novel classes.

Conclusions
Limitations.
Employing a graph neural network embedder, the proposed approach may inherit known issues such as the presence of information bottlenecks (Topping et al. 2021) and over smoothing. These may be aggravated by the additional aggregation required to compute the prototypes. The readout function to obtain a graph-level representation is already an aggregation of the node embeddings. Also, the nearest-neighbour association in the final embedding assumes that it enjoys a euclidean metric. While this is an excellent local approximation, we expect it may lead to imprecision. To overcome this, further improvements can be inspired by the Computer Vision community.
Future works.
In future work, we aim to enrich the latent space defined by the architecture, for instance, forcing the class prototypes in each episode to be sampled from a learnable distribution rather than directly computed as the mean of the supports. Moreover, it may be worth introducing an attention layer to have supports (or prototypes, directly) affect each other directly and not implicitly, as it now happens with the task embedding module. We also believe data augmentation is a crucial technique for the future of this task: the capacity to meaningfully inflate the small available datasets may result in a significant performance improvement. In this regard, we plan to extensively test the existing graph data augmentation techniques in the few-shot scenario and build upon MixUp to exploit different mixing strategies, such as non-linear interpolation.
Conclusions.
In this paper, we tackle the problem of FS graph classification, an under-explored problem in the broader machine learning community. The problem is particularly relevant in specialized domains such as biology and chemistry, given the nature of the samples to annotate. We propose a distance metric learning approach to tackle the problem, as samples embedded in a lower-dimensional space need fewer data to be discriminated. In this regard, we suggest adapting Prototypical Networks to the graph modality, showing that its simplicity does not undermine its effectiveness in the task. We then suggest valuable additions to the architecture, adapting a task-adaptive embedding procedure and designing a novel online graph data augmentation technique. Lastly, we prove their benefits for the problem over several datasets. We hope this work encourages researchers and practitioners to reconsider the effectiveness of distance metric learning when dealing with graph-structured data. In fact, we believe metric learning to be incredibly fit for dealing with graphs, considering that the latent spaces encoded by graph neural networks are known to capture both topological features and node signals efficaciously.